« Perl Weekly Challenge 164. Perl Weekly Challenge 166. »

Perl Weekly Challenge 165.

My solutions (task 1 and task 2 ) to the The Weekly Challenge - 165.

Task 1: Scalable Vector Graphics (SVG)

Submitted by: Ryan J Thompson

Scalable Vector Graphics (SVG) are not made of pixels, but
lines, ellipses, and curves, that can be scaled to any size
without any loss of quality. If you have ever tried to resize
a small JPG or PNG, you know what I mean by “loss of quality”!
What many people do not know about SVG files is, they are
simply XML files, so they can easily be generated
programmatically.

For this task, you may use external library, such as Perl’s
SVG library, maintained in recent years by our very own
Mohammad S Anwar. You can instead generate the XML yourself;
it’s actually quite simple. The source for the example image
for Task #2 might be instructive.

Your task is to accept a series of points and lines in the
following format, one per line, in arbitrary order:

Point: x,y

Line: x1,y1,x2,y2

Example:
53,10
53,10,23,30
23,30

Then, generate an SVG file plotting all points, and all
lines. If done correctly, you can view the output .svg file in
your browser.

This task comes right when I was trying to automate the generation of svg’s, as I learned that laser cutters may be driven through svg files. I’m planning a new version of my exposition ‘Light in Motion’ (Luz en Movimiento) using metallic plates instead of transparencies. I’ll write about it later. A couple of videos can be seen here and here.

I’ll translate Point: into an svg circle and Line: into an svg line. There are some subleties regarding the scale of the drawing, since I don’t know the range of the coordinates beforehand. I’ll comment the issues and my solution within the code. As I’m just learning about svg I guess better solutions may be found.

# Perl weekly challenge 165
# Task 1: Scalable vector graphics (svg)
#
# See https://wlmb.github.io/2022/05/20/PWC165/#task-1-scalable-vector-graphics-svg
use v5.12;
use warnings;
use SVG;
 8
# Parameter definitions
my $relative_radius=0.01; # size of point vs. canvas size
my $relative_width=0.005; # width of stroke vs. canvas size
my $absolute_size=400; # absolute size of canvas
my $fill="red"; # fill color
my $stroke="blue"; # stroke color
15
# Initialize svg object
my $svg=SVG->new(width=>$absolute_size, height=>$absolute_size);
18
# make group for transforming coordinates
my $g=$svg->group();
21
my @bbox; # required bounding box
while(<>){ # read input
    chomp;
    my @coords=split /\s*,\s*/; # interpret as comma separated coordinates
    # two coordinates for point, four for line
    die "Expected x,y or x1,y1,x2,y2 coordinates" unless @coords==2 || @coords==4;
    $g->circle(cx=>$coords[0], cy=>$coords[1], fill=>$fill) if @coords==2;
    $g->line(x1=>$coords[0],y1=>$coords[1],x2=>$coords[2],y2=>$coords[3], stroke=>$stroke)
        if @coords==4;
    adjust_bbox(@coords[(0,1)]); # acomodate bounding box to new coordinates
    adjust_bbox(@coords[(2,3)]);
}
my ($Lx, $Ly)=($bbox[2]-$bbox[0], $bbox[3]-$bbox[1]); # Get size of canvas in user coords.
$Lx||=1; # default size
$Ly||=1;
my $L=$Lx>$Ly?$Lx:$Ly; # make square canvas
my $radius=$relative_radius*$L; # radius of point
my $width=$relative_width*$L; # and stroke width in user coords
my $scale=$absolute_size/($L+2*$radius); # scale user to canvas coords
for(0,1){ # enlarge bounding box to accommodate radius of points at extremes
    $bbox[$_]-=$radius;
    $bbox[$_+2]=$bbox[$_]+$L+2*$radius;
}
# set radius of all circles
$_->setAttribute("r", $radius) for $g->getElements("circle");
# set stroke widths of all lines
$_->setAttribute("stroke-width", $width) for $g->getElements("line");
# set a coordinate transformation from user to canvas coordinates.
$g->setAttribute("transform", "scale($scale, -$scale) translate(".-$bbox[0].",".-$bbox[3].")");
say $svg->xmlify; # output the svg code
52
sub adjust_bbox { # enlarge the bounding box to accommodate a point
    my ($x, $y)=@_;
    return unless defined $x and defined $y;
    for ([0, $x, 1], [1, $y, 1], [2, $x, -1], [3, $y, -1]){
	my ($i,$z, $s)=@$_;
	$bbox[$i]=$z if !defined $bbox[$i] or $s*$z<$s*$bbox[$i];
    }
}
61

I took advantage of the capabilities of ŧhe package SVG::DOM, included by SVG, to set attributes of previously defined objects, as in lines 46, 48 and 50 of the script above. In svg increasing y in canvas coordinates corresponds to a downward motion. In line 50 I use a negative vertical scaling so that increasing y in user coordinates corresponds to an upward motion.

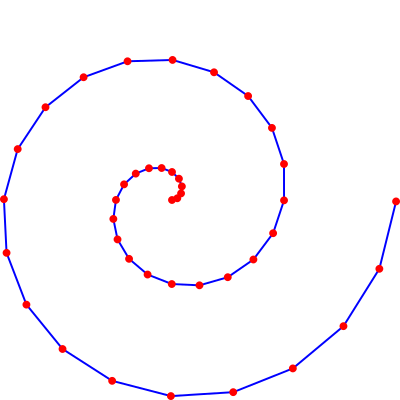
Example: I use a perl script to generate points along a spiral and feed them to my program.

perl -E ' ($r,$s)=(0,0);($p,$q,$r,$s)=($r,$s,$_*cos($_),$_*sin($_)),
say "$p,$q,$r,$s"  for map {$_*3.14/10} (1..40);
say $_*cos($_),",",$_*sin($_) for map {$_*3.14/10} (0..40);
'|./ch-1.pl >fig2.svg

Result (after conversion to png):

Task 2: Line of Best Fit

Submitted by: Ryan J Thompson

When you have a scatter plot of points, a line of best fit is
the line that best describes the relationship between the
points, and is very useful in statistics. Otherwise known as
linear regression, here is an example of what such a line
might look like:

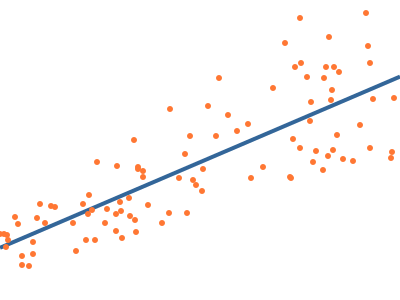
The method most often used is known as the least squares
method, as it is straightforward and efficient, but you may
use any method that generates the correct result.

Calculate the line of best fit for the following 48 points:

333,129  39,189 140,156 292,134 393,52  160,166 362,122  13,193
341,104 320,113 109,177 203,152 343,100 225,110  23,186 282,102
284,98  205,133 297,114 292,126 339,112 327,79  253,136  61,169
128,176 346,72  316,103 124,162  65,181 159,137 212,116 337,86
215,136 153,137 390,104 100,180  76,188  77,181  69,195  92,186
275,96  250,147  34,174 213,134 186,129 189,154 361,82  363,89

Using your rudimentary graphing engine from Task #1, graph all
points, as well as the line of best fit.

Given a set of N points (x_k,y_k), the least squares method chooses the optimum slope m and intercept b in order to minimize the sum of squared errors E=∑_k (y_k-m x_k-b)². Deriving E with respect to m and b and setting the partial derivatives to 0 yield the linear equations ∑_k (y_k-m x_k-b) x_k=0 and ∑_k (y_k-m x_k-b) =0, which may be written as (∑_k x_k²)m+(∑_k x_k) b=∑_k y_k x_k and (∑_k x_k)m + N b = ∑_k y_k, with solution m=(N∑_k y_k x_k-∑_k x_k ∑_l y_l)/(N∑_k x_k²-(∑_k x_k)²) and b=((∑_k x_k²)(∑_l y_l)-(∑_k x_k)(∑_l x_l y_l))/(N(∑_k x_k²)-(∑_k x_k)²).

I use the Perl Data Language (PDL) to process the input data. I evaluate the formulas above, although PDL has facilities for computing least squares fits.

perl -MPDL -E '$d=pdl($ARGV[0]); $N=$d->dim(1); $s=$d->transpose->sumover; ($sx, $sy)=$s->list;
$s2=($d**2)->transpose->sumover; ($sx2, $sy2)=$s2->list; $sxy=$d->prodover->sumover;
$m=($N*$sxy-$sx*$sy)/($N*$sx2-$sx**2); $b=($sx2*$sy-$sx*$sxy)/($N*$sx2-$sx**2);
say "m=$m, b=$b";
' "[[333,129],  [39,189], [140,156], [292,134], [393,52],  [160,166], [362,122],  [13,193],
    [341,104], [320,113], [109,177], [203,152], [343,100], [225,110], [23,186], [282,102],
    [284,98],  [205,133], [297,114], [292,126], [339,112], [327,79],  [253,136], [61,169],
    [128,176], [346,72],  [316,103], [124,162], [65,181], [159,137], [212,116], [337,86],
    [215,136], [153,137], [390,104], [100,180], [76,188],  [77,181],  [69,195],  [92,186],
    [275,96],  [250,147],  [34,174], [213,134], [186,129], [189,154], [361,82],  [363,89]]"

Results:

m=-0.299956500261231, b=200.132272535582

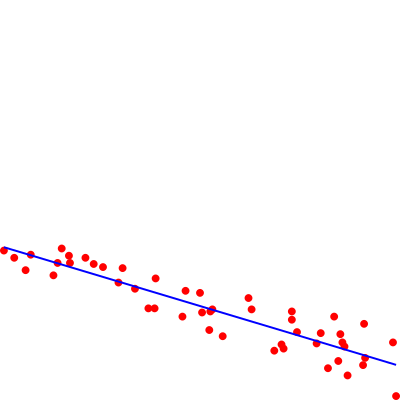
I modify the code to output the points and the adjusted line in a format that can be input to the previous program:

perl -MPDL -E '$d=pdl($ARGV[0]); $N=$d->dim(1); $s=$d->transpose->sumover; ($sx, $sy)=$s->list;
$s2=($d**2)->transpose->sumover; ($sx2, $sy2)=$s2->list; $sxy=$d->prodover->sumover;
$m=($N*$sxy-$sx*$sy)/($N*$sx2-$sx**2); $b=($sx2*$sy-$sx*$sxy)/($N*$sx2-$sx**2);
say join ",", @$_ for @{$d->unpdl}; $x=$d->slice("(0)"); ($x0,$x1)=($x->minimum,$x->maximum);
say sprintf "%f,%f,%f,%f", $x0, $m*$x0+$b,$x1,$m*$x1+$b;
' "[[333,129],  [39,189], [140,156], [292,134], [393,52],  [160,166], [362,122],  [13,193],
    [341,104], [320,113], [109,177], [203,152], [343,100], [225,110], [23,186], [282,102],
    [284,98],  [205,133], [297,114], [292,126], [339,112], [327,79],  [253,136], [61,169],
    [128,176], [346,72],  [316,103], [124,162], [65,181], [159,137], [212,116], [337,86],
    [215,136], [153,137], [390,104], [100,180], [76,188],  [77,181],  [69,195],  [92,186],
    [275,96],  [250,147],  [34,174], [213,134], [186,129], [189,154], [361,82],  [363,89]]
" | ./ch-1.pl >fig3.svg

Result:

The full code is

# Perl weekly challenge 165
# Task 2: Line of best fit
#
# See https://wlmb.github.io/2022/05/20/PWC165/#task-2-line-of-best-fit
use v5.12;
use warnings;
use PDL;
die 'Usage: ./ch-2.pl "[[x1,y1], [x2,y2]...]" to fit a set of points' unless @ARGV==1;
my $input=pdl($ARGV[0]);
my $N=$input->dim(1); # number of points
die 'Require more than one point' unless $N>1;
my $sum=$input->transpose->sumover;
my ($sum_x, $sum_y)=$sum->list;
my $sum_2=($input**2)->transpose->sumover; # sum of squares
my ($sum_x_2, $sum_y_2)=$sum_2->list;
my $sum_xy=$input->prodover->sumover; # sum of xy
my $det=$N*$sum_x_2-$sum_x**2;
die "Singular system" if $det==0;
my $slope=($N*$sum_xy-$sum_x*$sum_y)/$det;
my $intercept=($sum_x_2*$sum_y-$sum_x*$sum_xy)/$det;
say join ",", @$_ for @{$input->unpdl}; # output points
my $x=$input->slice("(0)"); # x coords
my ($y0, $y1)=map {$slope*$_+$intercept} (my ($x0,$x1)=($x->minimum,$x->maximum));
say "$x0, $y0, $x1, $y1";

Example:

./ch-2.pl "
    [[333,129],  [39,189], [140,156], [292,134], [393,52],  [160,166], [362,122],  [13,193],
    [341,104], [320,113], [109,177], [203,152], [343,100], [225,110], [23,186], [282,102],
    [284,98],  [205,133], [297,114], [292,126], [339,112], [327,79],  [253,136], [61,169],
    [128,176], [346,72],  [316,103], [124,162], [65,181], [159,137], [212,116], [337,86],
    [215,136], [153,137], [390,104], [100,180], [76,188],  [77,181],  [69,195],  [92,186],
    [275,96],  [250,147],  [34,174], [213,134], [186,129], [189,154], [361,82],  [363,89]]
" | ./ch-1.pl >fig4.svg

The resulting figure agrees with the previous one.

Written on May 20, 2022