Perl Weekly Challenge 146.
My solutions (task 1 and task 2 ) to the The Weekly Challenge - 146.
Task 1: 10001st Prime Number
Submitted by: Mohammad S Anwar
Write a script to generate the 10001st prime number.
We can borrow a canned solution, which yields a trivial oneliner.
perl -MMath::Prime::Util=nth_prime -E 'say nth_prime(10001)'
Results:
104743
A somewhat less cynical solution may be obtained by running an Erastothenes sieve on a large enough array and choosing the 10001’st term, which may be very compactly stated using the Perl Data Language (PDL).
perl -MPDL -MPDL::NiceSlice -E '$s=ones(120000);
$s(0:1).=0; $s($_*$_:-1:$_).=0 for(2..sqrt(120000-1));
$p=$s->xvals->where($s); say $p((10001-1))'
Here $s is a sieve, initialized to 1’s and set to zero for
all non-trivial multiples of previous numbers, and $p is the
array of primes. The result is:
104743
A more general solution follows, which takes as an optional argument the desired prime’s position.
1 # Perl weekly challenge 146
2 # Task 1: 10001st prime
3 #
4 # See https://wlmb.github.io/2022/01/03/PWC146/#task-1-10001st-prime
5 use v5.12;
6 use warnings;
7 use PDL;
8 use PDL::NiceSlice;
9 use Try::Tiny;
10 for my $N(@ARGV?@ARGV:10001){
11 try{
12 die "Argument $N is not positive\n" unless $N>=1;
13 # Estimate size $M of required sieve by solving $M/log($M) approx $N
14 # unless $N is too small
15 my $M=$N<4?6:find_zero(sub {my $x=shift; $N-$x/log($x)},
16 sub {my $l=log($_[0]); 1/$l**2-1/$l}, $N);
17 my $sieve=ones($M); # fill sieve with ones
18 $sieve(0:1).=0; # 0 and 1 are not primes
19 $sieve($_*$_:-1:$_).=0 foreach(2..sqrt($M-1)); # multiples of 'it' are not prime
20 my $primes=$sieve->xvals->where($sieve); # first primes
21 die "Short sieve" unless $N<=$primes->nelem; # shouldn't happen
22 my $Nth=$N>1?"$N-th":"$N-st";
23 say "The $Nth prime is ", $primes(($N-1));
24 }
25 catch { say $_;}
26 }
27
28 no PDL::NiceSlice; # NiceSlice destroys indirect function calls!
29 sub find_zero { # Find zero of function using Newton's iteration
30 my ($f, $d, $x0)=@_; # function, derivative, initial guess
31 my $x=$x0;
32 my $y;
33 my $max=10; # guard against non-convergence
34 do{($y, $x)= ($x, $x-$f->($x)/$d->($x))} until approx($y,$x) or --$max<=0;
35 die "find_zero didn't converge starting from $x0\n" unless $max>0;
36 return $x;
37 }
38
Example:
./ch-1.pl
Results:
The 10001-th prime is 104743
Other examples:
./ch-1.pl 11 101 1001 10001 100001
Results:
The 11-th prime is 31
The 101-th prime is 547
The 1001-th prime is 7927
The 10001-th prime is 104743
The 100001-th prime is 1299721
Example with an error:
./ch-1.pl 0 1
Results:
Argument 0 is not positive
The 1-st prime is 2
Task 2: Curious Fraction Tree
Submitted by: Mohammad S Anwar
Consider the following Curious Fraction Tree:
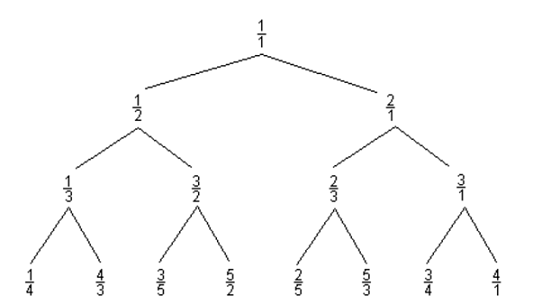
You are given a fraction, member of the tree created similar
to the above sample.
Write a script to find out the parent and grandparent of the
given member.
Example 1:
Input: $member = '3/5';
Output: parent = '3/2' and grandparent = '1/2'
Example 2:
Input: $member = '4/3';
Output: parent = '1/3' and grandparent = '1/2'
The tree grows by adding the numerator and denominator and
substituting the result for the denominator (left branches)
and for the numerator (right branches). Thus, consider
n/m. Its parent should be (n-m)/m if m<n, and n/(m-n)
if n<m. A simple solution is the one-liner
perl -E 'sub p{my ($n,$d)=@_; return $d>$n?($n,$d-$n):($n-$d,$d)} @gp=p(@p=p(@ARGV));
say "Input: $ARGV[0]/$ARGV[1], Parent: $p[0]/$p[1], Grandparent: $gp[0]/$gp[1]"' 3 5
perl -E 'sub p{my ($n,$d)=@_; return $d>$n?($n,$d-$n):($n-$d,$d)} @gp=p(@p=p(@ARGV));
say "Input: $ARGV[0]/$ARGV[1], Parent: $p[0]/$p[1], Grandparent: $gp[0]/$gp[1]"' 4 3
Results:
Input: 3/5, Parent: 3/2, Grandparent: 1/2
Input: 4/3, Parent: 1/3, Grandparent: 1/2
If n=m then we are already at the root of the
tree. The tree only contains reduced fractions, so I might
have to cancel out common factors. Thus a full solution would
be:
1 # Perl weekly challenge 146
2 # Task 2: Curious Fraction Tree
3 #
4 # See https://wlmb.github.io/2022/01/03/PWC146/#task-2-curious-fraction-tree
5 use v5.12;
6 use warnings;
7 use Try::Tiny;
8 foreach(@ARGV){
9 try {
10 my($n, $d)=($1,$2) if m{^\s*(\d+)\s*/\s*(\d+)\s*$};
11 die "Wrong argument $_\n" unless defined $n and defined $d;
12 die "Numerator and denominator in $_ should be positive\n"
13 unless $n>0 and $d>0;
14 my $gcd=gcd($n, $d);
15 say "Warning: $_ not reduced" unless $gcd==1;
16 ($n, $d)=map {$_/$gcd} ($n, $d);
17 my @parent=parent($n, $d);
18 try {
19 my @grand_parent=parent(@parent);
20 say "Input: $n/$d\nParent:$parent[0]/$parent[1]\n",
21 "Grand parent: $grand_parent[0]/$grand_parent[1]\n";
22 }
23 catch {
24 die "No grandparent of $n/$d\n";
25 }
26 }
27 catch {
28 say $_;
29 }
30 }
31
32 sub gcd {
33 my ($n, $m)=@_;
34 ($n, $m)=($m, $n%$m) while ($m);
35 return $n;
36 }
37 sub parent {
38 my ($n, $d)=@_;
39 die "No parent of $n/$d\n" if $n==$d;
40 return $d>$n?($n,$d-$n):($n-$d,$d);
41 }
42
I used the try/catch mechanism from Try::Tiny module to
recover from errors when present.
Examples:
./ch-2.pl 3/5 4/3
Results:
Input: 3/5
Parent:3/2
Grand parent: 1/2
Input: 4/3
Parent:1/3
Grand parent: 1/2
Some examples with errors:
./ch-2.pl 0/1 1/1 1/2 24/16 22/22 2 2.5/4.3
Results:
Numerator and denominator in 0/1 should be positive
No parent of 1/1
No grandparent of 1/2
Warning: 24/16 not reduced
Input: 3/2
Parent:1/2
Grand parent: 1/1
Warning: 22/22 not reduced
No parent of 1/1
Wrong argument 2
Wrong argument 2.5/4.3