Perl Weekly Challenge 121.
My solutions (task 1, task 2, task 2 (helper), task 2a, and task 2b) to the The Weekly Challenge - 121.
Task 1: Invert Bit
Submitted by: Mohammad S Anwar
You are given integers 0 <= $m <= 255 and 1 <= $n <= 8.
Write a script to invert $n bit from the end of the binary
representation of $m and print the decimal representation of
the new binary number.
Example
Input: $m = 12, $n = 3
Output: 8
Binary representation of $m = 00001100
Invert 3rd bit from the end = 00001000
Decimal equivalent of 00001000 = 8
Input $m = 18, $n = 4
Output: 26
Binary representation of $m = 00010010
Invert 4th bit from the end = 00011010
Decimal equivalent of 00011010 = 26
The truth table of the xor (^) operator is
| a | b | a ^ b |
|---+---+-------|
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 0 |
When a==0 the first two rows show that a^b==b, and when
a=1 the last two rows show that a^b==!b. Thus, we can
invert a bit by xoring with a word that has that bit on and
all the rest turned off. This yields a one liner:
perl -MList::Util=pairs -E 'foreach(pairs @ARGV){($n,$b)=@$_; \
say "Number: $n, Bit: $b Output: ", (1<<($b-1))^$n;}' 12 3 18 4
Results:
Number: 12, Bit: 3 Output: 8
Number: 18, Bit: 4 Output: 26
The full version:
# Perl weekly challenge 121
# Task 1: Invert bit
#
# See https://wlmb.github.io/2021/07/12/PWC121/#task-1-invert-bit
use strict;
use warnings;
use v5.12;
use List::Util qw(pairs);
use POSIX qw(round);
foreach(pairs @ARGV){
my ($n,$b)=map {round $_} @$_; # Assure integer
say("Wrong range: 0<=$n<=255 && 1<=$b<=8?"), next
unless 0<=$n<=255 && 1<=$b<=8; # ??
my $r=(1<<($b-1))^$n; # Count bits from 1, not 0
say "Number: $n, Bit: $b, Output: $r";
}
Example:
./ch-1.pl 12 3 18 4 300 25
Results:
Number: 12, Bit: 3, Output: 8
Number: 18, Bit: 4, Output: 26
Wrong range: 0<=300<=255 && 1<=25<=8?
Task 2: The Traveling Salesman
Submitted by: Jorg Sommrey
You are given a NxN matrix containing the distances between N
cities.
Write a script to find a round trip of minimum length visiting
all N cities exactly once and returning to the start.
Example
Matrix: [0, 5, 2, 7]
[5, 0, 5, 3]
[3, 1, 0, 6]
[4, 5, 4, 0]
Output:
length = 10
tour = (0 2 1 3 0)
BONUS 1: For a given number N, create a random NxN distance
matrix and find a solution for this matrix.
BONUS 2: Find a solution for a random matrix of size 15x15 or
20x20
Exhaustive search
This is a hard one (for the computer). The easy (for the programmer) solution is to generate all tours, choosing the shortest one.
# Perl weekly challenge 121
# Task 2: The traveling salesman
#
# See https://wlmb.github.io/2021/07/12/PWC121/#task-2-the-traveling-salesman
use strict;
use warnings;
use v5.12;
use PDL; # Perl data language
foreach(@ARGV){
#Assume the matrix is of the form [[m00,m01,m02..],[m10,m11,...]...]
my $M=pdl($_);
say("Require square matrix"), next unless $M->ndims==2 and $M->dim(0)==$M->dim(1);
say("Self distances should be null"), next unless all($M->diagonal(0,1)==0);
my $N=$M->dim(0); # number of cities
my $iterate=permutator($N);
my $best_tour;
my $shortest_length;
while(my @cities=$iterate->()){ # for each possible trip
my $tour=pdl(@cities);
my $indices=pdl($tour->rotate(-1), $tour)->transpose; #pair next city to current city
my $length=$M->indexND($indices)->sumover; # get distances for this trip and sum
($best_tour, $shortest_length)=($tour, $length)
if !defined $shortest_length || $length<$shortest_length;
}
$best_tour=append($best_tour,0); #go back to the first city
say "\nInput $M\nBest tour: $best_tour\nShortest length: $shortest_length";
say("Strange metric: Length A->B not equal Length B->A")
unless all $M==$M->transpose;
}
I recycle the iterator I used for the task 2 of PWC109 with some small variations. I arbitrarily choose to start and end at city number 0.
sub permutator { #returns an iterator for permutations
my $n_items=(shift)-1;
my @items=1..$n_items;
my $n=0;
my $done=0;
sub {
return if $done;
my $which=$n; #next item to transpose
return 0,@items if $n++ == 0; #return first time through
my $with_whom=1; #with whom to permute
while($with_whom<=$n_items&&$which%$with_whom==0){
$which/=$with_whom;
++$with_whom;
}
$done=1, return if $with_whom >$n_items; #no more transpositions
$which=$with_whom-$which%$with_whom;
#use negative indices to transpose rightmost first
@items[-$with_whom+1..-1]=reverse @items[-$with_whom+1..-1]; #reorder
@items[-$which,-$with_whom]=@items[-$with_whom,-$which]; # transpose
return 0,@items
}
}
Examples:
./ch-2.pl '[[0, 5, 2, 7],[5, 0, 5, 3],[3, 1, 0, 6],[4, 5, 4, 0]]' \
'[[0,2,3],[20,0,6],[30,60,0]]'
Results:
Input
[
[0 5 2 7]
[5 0 5 3]
[3 1 0 6]
[4 5 4 0]
]
Best tour: [0 2 1 3 0]
Shortest length: 10
Strange: Length A->B not equal Length B->A
Input
[
[ 0 2 3]
[20 0 6]
[30 60 0]
]
Best tour: [0 1 2 0]
Shortest length: 38
Strange: Length A->B not equal Length B->A
Generate random distances
There are bonus points for generating random matrices and computing the corresponding optimal trip. This could be accomplished with a small auxiliary program to produce and format the random matrix.
# Perl weekly challenge 121
# Task 2: The traveling salesman. Auxiliary program
#
# See https://wlmb.github.io/2021/07/12/PWC121/#task-2-the-traveling-salesman
use strict;
use warnings;
use v5.12;
use PDL;
foreach(@ARGV){
my $m=random($_,$_);
$m->diagonal(0,1).=0; # zero the diagonal
$m= ($m+$m->transpose)/2; #symmetrize (?)
# Format:
print "\'[", join(',', map {'['. join(',', @$_).']'} @{unpdl $m}), "]\' ";
}
I use this program to feed the previous one.
time (./ch-2-helper.pl 9 |xargs ./ch-2.pl) 2>&1
Results:
Input
[
[ 0 0.22770941 0.14699538 0.37362833 0.19222196 0.43112944 0.30877502 0.72697343 0.51947665]
[0.22770941 0 0.56474448 0.50425302 0.47321854 0.37131508 0.23933324 0.55066754 0.30271257]
[0.14699538 0.56474448 0 0.67341537 0.79956918 0.50607642 0.67658632 0.13525839 0.81253649]
[0.37362833 0.50425302 0.67341537 0 0.39963737 0.70170315 0.72623112 0.18561545 0.56249972]
[0.19222196 0.47321854 0.79956918 0.39963737 0 0.16108423 0.39777427 0.1003624 0.59775856]
[0.43112944 0.37131508 0.50607642 0.70170315 0.16108423 0 0.59901288 0.77626906 0.66784913]
[0.30877502 0.23933324 0.67658632 0.72623112 0.39777427 0.59901288 0 0.78968984 0.19305438]
[0.72697343 0.55066754 0.13525839 0.18561545 0.1003624 0.77626906 0.78968984 0 0.48100651]
[0.51947665 0.30271257 0.81253649 0.56249972 0.59775856 0.66784913 0.19305438 0.48100651 0]
]
Best tour: [0 2 7 3 8 6 1 5 4 0]
Shortest length: 2.18737782278835
real 0m2.836s
user 0m2.803s
sys 0m0.034s
From the timing of the example above we can estimate how long
it would take with this algorithm for an N=15 or N=20
trip, as the time goes with the number possible trips, i.e.,
the number of permutations of N-1 cities (the first city is
arbitrary but fixed), given by the factorial function
(N-1)!. Thus, given that for N=9 it took about 3s, for
N=15 it would take about 3s*14!/8!=6486480s=75 days, and for
N=20 about three hundred thousand years.
Simulated annealing
Alternatives to the exhaustive search for an optimum include using some heuristics or maybe just choosing a random first candidate and then using a suboptimal but realizable optimization such as simulated annealing, which yields good but in general not optimum solutions. For example, one could use the Monte Carlo method, permuting two randomly chosen cities, computing the change of length ΔL, and accepting the new configuration if ΔL≤0, or accepting it with probability exp(-ΔL/L0) if ΔL>0, where L0 plays the role of a temperature that is gradually decreased. In the limit L0→0, this procedure would yield a local minimum. The higher the starting value of L0 and the slower its decrease, the closer the length of the solution would be to that of the true optimum.
# Perl weekly challenge 121
# Task 2: The traveling salesman. Simulated Annealing
#
# See https://wlmb.github.io/2021/07/12/PWC121/#task-2-the-traveling-salesman
use strict;
use warnings;
use v5.12;
use PDL;
die "Usage: ./ch-2a.pl cities steps high low output" unless @ARGV==5;
my ($cities, $steps, $high, $low, $output)=@ARGV;
open(my $fh, '>', $output) or die "Couldn't open $output: $!";
srand(0); #seed, for tests
my $M=random($cities, $cities); # generate distances matrix
$M->diagonal(0,1).=0; # zero the diagonal
$M= ($M+$M->transpose)/2; #symmetrize (?)
my $L0=$high; # starting 'temperature'
my $L_stop=$low;
my $factor=($low/$high)**(1/$steps);
my $route=pdl(0..$cities-1); #initial route
my $L=distance($route);
while($L0>$L_stop){
my $new_route=step($route);
my $new_L=distance($new_route);
my $dL=$new_L-$L;
if($dL<=0 || random(1)<exp(-$dL/$L0)){
$route=$new_route; # accept
$L=$new_L;
}
say $fh $L; # for plotting later
$L0*=$factor;
}
my $best_route=append($route, 0);
say "Distance table: $M\nSteps: $steps\nCities: $cities\nRoute: $best_route\nLength: $L";
sub step {
my $i=random(2)*($cities-1)+1;
my $new_route=$route->copy;
$new_route->index($i).=$new_route->index($i->rotate(1));
return $new_route;
}
sub distance {
my $r=shift;
my $indices=pdl($r->rotate(-1),$r)->transpose;
return $M->indexND($indices)->sumover;
}
Examples:
./ch-2a.pl 9 100000 1 .01 rem.txt
Results:
Distance table:
[
[ 0 0.74749854 0.40595513 0.51682737 0.30143922 0.77794547 0.59730636 0.66476384 0.92926051]
[0.74749854 0 0.21836622 0.50401428 0.20721647 0.25084233 0.73211532 0.49470507 0.57587914]
[0.40595513 0.21836622 0 0.18515395 0.46370522 0.58086441 0.50233819 0.70287476 0.86681642]
[0.51682737 0.50401428 0.18515395 0 0.29532967 0.74732821 0.36795896 0.20339507 0.54525895]
[0.30143922 0.20721647 0.46370522 0.29532967 0 0.54774407 0.50358504 0.60824515 0.61137246]
[0.77794547 0.25084233 0.58086441 0.74732821 0.54774407 0 0.52216738 0.50350537 0.79060438]
[0.59730636 0.73211532 0.50233819 0.36795896 0.50358504 0.52216738 0 0.51522601 0.10107789]
[0.66476384 0.49470507 0.70287476 0.20339507 0.60824515 0.50350537 0.51522601 0 0.95504256]
[0.92926051 0.57587914 0.86681642 0.54525895 0.61137246 0.79060438 0.10107789 0.95504256 0]
]
Steps: 100000
Cities: 9
Route: [0 2 3 7 6 8 5 1 4 0]
Length: 2.96091044611578
We can check the result above by using the exhaustive search,
./ch-2.pl '[[0,0.74749854,0.40595513,0.51682737,0.30143922,0.77794547,0.59730636,0.66476384,0.92926051],[0.74749854,0,0.21836622,0.50401428,0.20721647,0.25084233,0.73211532,0.49470507,0.57587914],[0.40595513,0.21836622,0,0.18515395,0.46370522,0.58086441,0.50233819,0.70287476,0.86681642],[0.51682737,0.50401428,0.18515395,0,0.29532967,0.74732821,0.36795896,0.20339507,0.54525895],[0.30143922,0.20721647,0.46370522,0.29532967,0,0.54774407,0.50358504,0.60824515,0.61137246],[0.77794547,0.25084233,0.58086441,0.74732821,0.54774407,0,0.52216738,0.50350537,0.79060438],[0.59730636,0.73211532,0.50233819,0.36795896,0.50358504,0.52216738,0,0.51522601,0.10107789],[0.66476384,0.49470507,0.70287476,0.20339507,0.60824515,0.50350537,0.51522601,0,0.95504256],[0.92926051,0.57587914,0.86681642,0.54525895,0.61137246,0.79060438,0.10107789,0.95504256,0]]'
Results:
Input
[
[ 0 0.74749854 0.40595513 0.51682737 0.30143922 0.77794547 0.59730636 0.66476384 0.92926051]
[0.74749854 0 0.21836622 0.50401428 0.20721647 0.25084233 0.73211532 0.49470507 0.57587914]
[0.40595513 0.21836622 0 0.18515395 0.46370522 0.58086441 0.50233819 0.70287476 0.86681642]
[0.51682737 0.50401428 0.18515395 0 0.29532967 0.74732821 0.36795896 0.20339507 0.54525895]
[0.30143922 0.20721647 0.46370522 0.29532967 0 0.54774407 0.50358504 0.60824515 0.61137246]
[0.77794547 0.25084233 0.58086441 0.74732821 0.54774407 0 0.52216738 0.50350537 0.79060438]
[0.59730636 0.73211532 0.50233819 0.36795896 0.50358504 0.52216738 0 0.51522601 0.10107789]
[0.66476384 0.49470507 0.70287476 0.20339507 0.60824515 0.50350537 0.51522601 0 0.95504256]
[0.92926051 0.57587914 0.86681642 0.54525895 0.61137246 0.79060438 0.10107789 0.95504256 0]
]
Best tour: [0 2 3 7 6 8 5 1 4 0]
Shortest length: 2.96091045
So it seems that the simple simulated annealing is up to the job. To
understand how the system converges I plot the result vs. the number
of steps using gnuplot.
reset
set xlabel 'Number of steps'
set ylabel 'Length'
set title 'Cities: 9 Sim. annealing factor: 1->0.01'
unset key
plot 'rem.txt' u (10*$0):1 every 10 w l

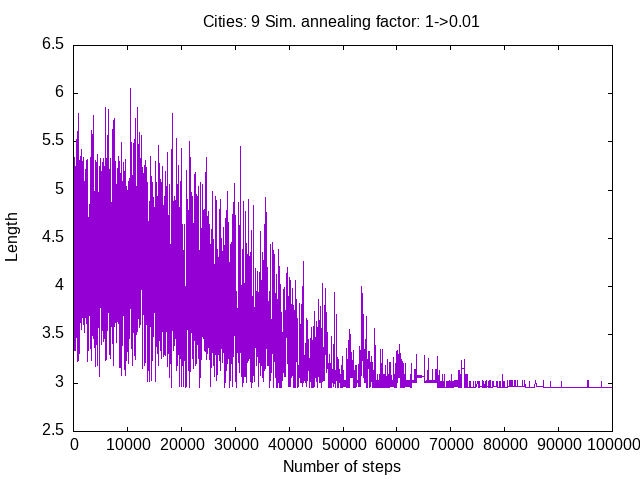
Now I go ahead and attempt a larger trip, with 20 cities.
./ch-2a.pl 20 100000 1 .01 rem1.txt
Results:
Distance table:
[
[ 0 0.60286355 0.31285254 0.66694544...]
[ 0.60286355 0 0.71103826 0.51146518...]
[ . . . . ...]
[ . . . . ...]
[ . . . . ...]
]
Steps: 100000
Cities: 20
Route: [0 13 9 5 17 12 8 4 7 6 2 14 18 3 10 11 15 16 1 19 0]
Length: 4.6194812068939
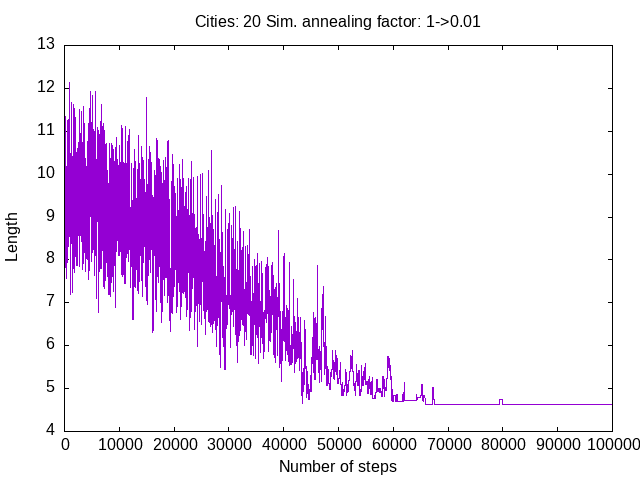
So the simulation seems to be well converged.
Realistic distances
A problem with the programs above with regards to the traveling salesman problem is that the random distances are unrealistic. I would expect any set of distances computed with any metric, say, the real geometric distance given by the Euclidean L2 metric or the distance along the streets of a cuadriculated city given by the L1 norm, to obey the triangle inequality dAB+dBC ≥ dAC. The random numbers I’ve been using above violate this inequality in general. Two cities that are close to a third ought to be close among themselves. That is not the case for randomly assigned distances. Thus, I rewrite the program above but using randomly positioned cities and calculating their acutal geometric distance, using some PDL shorcuts. After initializing the distance matrix the rest of the program is identical.
# Perl weekly challenge 121
# Task 2: The traveling salesman. Simulated Annealing. Obeying triangle inequality.
#
# See https://wlmb.github.io/2021/07/12/PWC121/#task-2-the-traveling-salesman
use strict;
use warnings;
use v5.12;
use PDL;
die "Usage: ./ch-2a.pl cities steps high low output" unless @ARGV==5;
my ($cities, $steps, $high, $low, $output)=@ARGV;
open(my $fh, '>', $output) or die "Couldn't open $output: $!";
srand(0); #seed, for tests
my $locations=random(2,$cities); #positions of cities in a plane
my $M=(($locations->dummy(2)-$locations->dummy(1))**2)->sumover->sqrt; # euclidean distances
my $L0=$high; # starting 'temperature'
my $L_stop=$low;
my $factor=($low/$high)**(1/$steps);
my $route=pdl(0..$cities-1); #initial route
my $L=distance($route);
while($L0>$L_stop){
my $new_route=step($route);
my $new_L=distance($new_route);
my $dL=$new_L-$L;
if($dL<=0 || random(1)<exp(-$dL/$L0)){
$route=$new_route; # accept
$L=$new_L;
}
say $fh $L;
$L0*=$factor;
}
my $best_route=append($route, 0);
say "Distance table: $M\nSteps: $steps\nCities: $cities\nRoute: $best_route\nLength: $L";
sub step {
my $i=random(2)*($cities-1)+1;
my $new_route=$route->copy;
$new_route->index($i).=$new_route->index($i->rotate(1));
return $new_route;
}
sub distance {
my $r=shift;
my $indices=pdl($r->rotate(-1),$r)->transpose;
return $M->indexND($indices)->sumover;
}
Example:
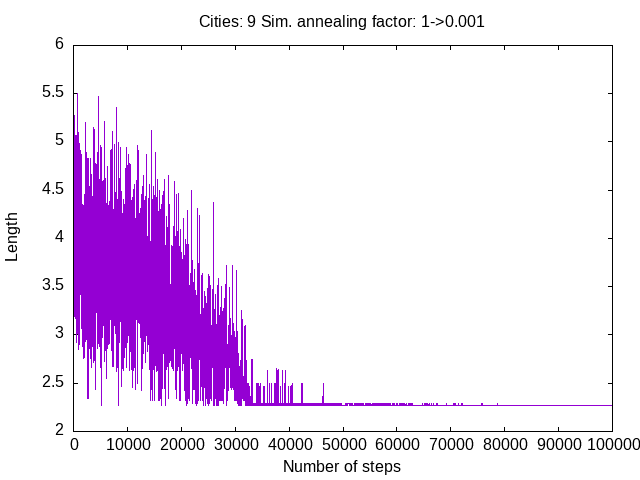
./ch-2b.pl 9 100000 1 .001 rem2.txt
Results:
Distance table:
[
[ 0 0.14170127 0.4080575 0.64582278 0.70309247 0.48238837 0.74517376 0.22507754 0.69632666]
[0.14170127 0 0.48832752 0.77891353 0.78757497 0.62393047 0.881522 0.31230217 0.80456918]
[ 0.4080575 0.48832752 0 0.4325695 0.29938057 0.45156833 0.54801779 0.18323136 0.34027176]
[0.64582278 0.77891353 0.4325695 0 0.41790176 0.24660718 0.11579293 0.50520091 0.25732945]
[0.70309247 0.78757497 0.29938057 0.41790176 0 0.579854 0.50506582 0.48065643 0.17175052]
[0.48238837 0.62393047 0.45156833 0.24660718 0.579854 0 0.30134798 0.42621535 0.45662134]
[0.74517376 0.881522 0.54801779 0.11579293 0.50506582 0.30134798 0 0.61744569 0.33502502]
[0.22507754 0.31230217 0.18323136 0.50520091 0.48065643 0.42621535 0.61744569 0 0.49352759]
[0.69632666 0.80456918 0.34027176 0.25732945 0.17175052 0.45662134 0.33502502 0.49352759 0]
]
Steps: 100000
Cities: 9
Route: [0 1 7 2 4 8 3 6 5 0]
Length: 2.26522461437601
I compare it to the optimum
./ch-2.pl [[0,0.14170127,0.4080575,0.64582278,0.70309247,0.48238837,0.74517376,0.22507754,0.69632666],[0.14170127,0,0.48832752,0.77891353,0.78757497,0.62393047,0.881522,0.31230217,0.80456918],[0.4080575,0.48832752,0,0.4325695,0.29938057,0.45156833,0.54801779,0.18323136,0.34027176],[0.64582278,0.77891353,0.4325695,0,0.41790176,0.24660718,0.11579293,0.50520091,0.25732945],[0.70309247,0.78757497,0.29938057,0.41790176,0,0.579854,0.50506582,0.48065643,0.17175052],[0.48238837,0.62393047,0.45156833,0.24660718,0.579854,0,0.30134798,0.42621535,0.45662134],[0.74517376,0.881522,0.54801779,0.11579293,0.50506582,0.30134798,0,0.61744569,0.33502502],[0.22507754,0.31230217,0.18323136,0.50520091,0.48065643,0.42621535,0.61744569,0,0.49352759],[0.69632666,0.80456918,0.34027176,0.25732945,0.17175052,0.45662134,0.33502502,0.49352759,0]]
Results:
Input
[
[ 0 0.14170127 0.4080575 0.64582278 0.70309247 0.48238837 0.74517376 0.22507754 0.69632666]
[0.14170127 0 0.48832752 0.77891353 0.78757497 0.62393047 0.881522 0.31230217 0.80456918]
[ 0.4080575 0.48832752 0 0.4325695 0.29938057 0.45156833 0.54801779 0.18323136 0.34027176]
[0.64582278 0.77891353 0.4325695 0 0.41790176 0.24660718 0.11579293 0.50520091 0.25732945]
[0.70309247 0.78757497 0.29938057 0.41790176 0 0.579854 0.50506582 0.48065643 0.17175052]
[0.48238837 0.62393047 0.45156833 0.24660718 0.579854 0 0.30134798 0.42621535 0.45662134]
[0.74517376 0.881522 0.54801779 0.11579293 0.50506582 0.30134798 0 0.61744569 0.33502502]
[0.22507754 0.31230217 0.18323136 0.50520091 0.48065643 0.42621535 0.61744569 0 0.49352759]
[0.69632666 0.80456918 0.34027176 0.25732945 0.17175052 0.45662134 0.33502502 0.49352759 0]
]
Best tour: [0 1 7 2 4 8 3 6 5 0]
Shortest length: 2.26522462
I got the same solution. I plot below the evolution of the simulation.
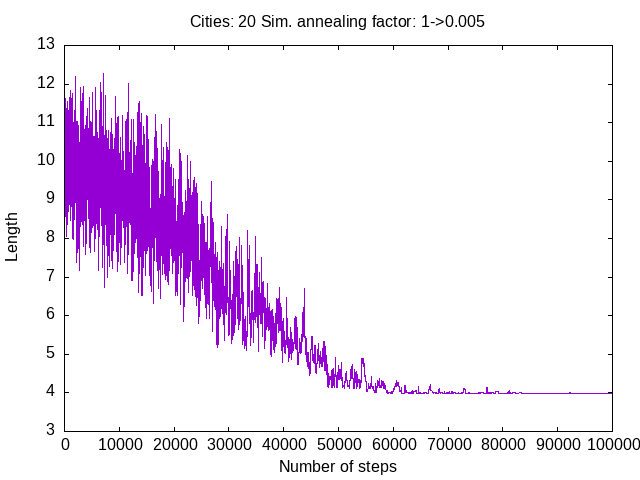
I try now the case of 20 cities.
./ch-2b.pl 20 100000 1 .005 rem3.txt
Results:
Distance table:
[
[ 0 0.14170127 0.4080575 0.64582278 0.70309247 0.48238837 ...]
[ 0.14170127 0 0.48832752 0.77891353 0.78757497 0.62393047 ...]
[ 0.4080575 0.48832752 0 0.4325695 0.29938057 0.45156833 ...]
[ 0.64582278 0.77891353 0.4325695 0 0.41790176 0.24660718 ...]
[ 0.70309247 0.78757497 0.29938057 0.41790176 0 0.579854 ...]
[ 0.48238837 0.62393047 0.45156833 0.24660718 0.579854 0 ...]
[ . . . . . , ...]
[ . . . . . , ...]
[ . . . . . , ...]
[ . . . . . , ...]
]
Steps: 100000
Cities: 20
Route: [0 18 14 19 10 5 11 3 6 9 16 13 15 8 4 2 12 7 17 1 0]
Length: 3.98729459557798
And I plot the convergence.
I can attempt much larger problems, such as visiting 100 cities.
./ch-2b.pl 100 100000 1 .005 rem4.txt
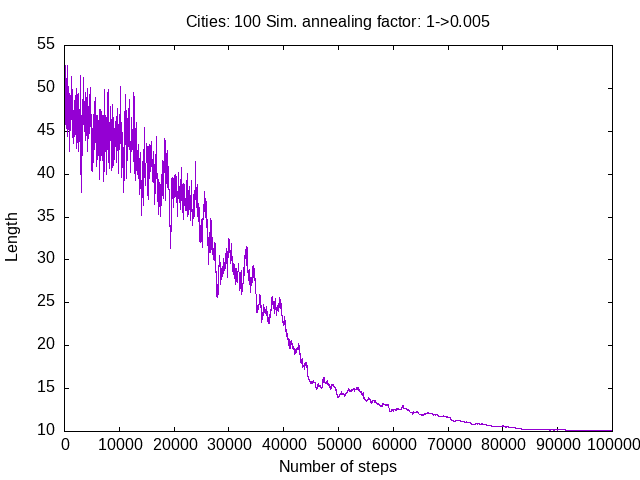
In summary, with the simulated annealing algorithm presented above one can search in a few seconds for good solutions to the traveling salesman problem. For small problems, the solutions coincided with the truly optimal ones, but that would not be the case in general. The results depend on the parameters of the simulation such as the starting and ending temperature and the rate of cooling. Simulated annealing and other related methods like genetic algorithms or ant colony optimization are useful for obtaining adequate solutions to problems for which an exhaustive search for an optimum would be prohibitively expensive, such as the traveling salesman problem.