Efecto de campo local superficial
Introducción
( Si encuentra las ecuaciones ilegibles en esta versión, puede consultar la versión pdf con las ecuaciones bien tipografiadas aquí )
La respuesta macroscópica de un sistema no es el simple promedio de su
respuesta microscópica. Esto se debe a que el campo eléctrico
microscópico tiene fluctuaciones espaciales que están correlacionadas
con la textura espacial del sistema. Este efecto es conocido como el
efecto de campo local. Un ejemplo muy conocido de este efecto es el
de un sólido isotrópico modelado como una red cúbica de entidades
polarizables puntuales caracterizadas por su polarizabilidad
. Sin efecto de campo local, la respuesta dieléctrica
macroscópica sería
1
con 
la densidad de
las entidades polarizables. Sin embargo, al tomar en cuenta que la
polarizabilidad es la respuesta no sólo al campo externo, sino también
al campo producido por todos los dipolos vecinos, la ecuación anterior
se ve reemplazada por la relación de Claussius-Mossoti,
2
3
Como la corrección de campo local depende de la interacción con entidades polarizables vecinas, podríamos esperar que se vea modificada en la vecindad de una superficie. El propósito de estas notas es mostrar cómo podríamos calcular el efecto de campo local superficial y explorar sus consecuencias.
Teoría
Consideremos una red de Bravais bidimensional 
en el plano
ocupada por
cargas puntuales unitarias 
. El potencial electrostático
que
produciría en un punto 
es
4
La ecuación previa no es muy útil por la lenta convergencia en el espacio real del potencial Coulombiano. Conviene entonces recurrir a la ecuación diferencial del potencial,
5
en el espacio recíproco 
definido por 
,
6
con 
es el coeficiente de Fourier 2D del potencial
evaluado a la altura 
.
La solución que decae al alejarnos del plano para 
es
7
Regresando al espacio real, el potencial queda dado por
8
donde añadimos al termino 
correspondiente al potencial producido
por una película uniformemente cargada, y dónde introdujimos los
vectores
9
y empleamos el signo 
cuando 
y el signo 
cuando
. Esta es una serie rápidamente convergente siempre y cuando
.
Consideremos ahora la misma red de Bravais, pero ocupada por
dipolos idénticos 
. La densidad de carga sería entonces
10
i.e., operamos sobre la densidad monopolar con el operador 
. Luego,
el potencial dipolar 
se obtiene aplicando el mismo
operador sobre el potencial monopolar, 
,
11
y el campo eléctrico 
,
12
Construyamos ahora un cristal con caras planas orientadas de acuerdo a alguna dirección cristalográfica. La ecuación que obedece la -ésima entidad polarizable es
13
donde 
representa el campo eléctrico en el
sitio 
producido por un dipolo que 
en el sitio
. Suponiendo que todos los dipolos de un plano son equivalentes,
podemos podemos sumar las interacciones por planos
cristalinos. Definimos entonces
14
donde es un sitio cualquiera del plano . Usando el campo
dipolar previo,
la interacción entre planos cristalinos está dada por el tensor
15
donde 
son vectores recíprocos bidimensionales, 
es
un vector que va de un sitio del plano 
a uno del plano 
, y
donde usamos el signo cuando 
y el signo cuando 
.
Para el caso 
podemos usar la regla de suma
16
en el bulto del sistema, con la densidad de entidades
polarizables, y despejar 
(sin suma), la autointeracción
dipolar de un plano.
Interacciones
Empezamos por cargar librerías y opciones.
# name: init
use strict;
use warnings;
use v5.12;
use Getopt::Long; # Read options
use Scalar::Util qw(looks_like_number);
use Exporter::Renaming;
use List::Util Renaming=>[all=>'lu_all']; # Rename all method
use PDL; # Perl Data Language
use PDL::NiceSlice;
use PDL::Constants qw(PI);
Necesitamos una rutina para mandar mensajes de error y medio explicar el uso del programa.
# name: usage
sub usage($$) {
my ($options, $message)=@_;
say $message;
say $options;
exit 1;
}
También requrimos algunas rutinas de utilería. Definimos el producto
escalar (no hermitiano) entre vectores posiblemente
complejos. (La rutina de PDL no sabe aún qué hacer con complejos)
# name: cinner
sub cinner($$) {
my ($a,$b)=@_;
return ($a*$b)->sumover;
}
Otra rutina de utilería para acotar el número de dígitos decimales a imprimir.
# name: trunc
sub trunc($@) {
my $size=shift; # how many decimal digits to keep
my @a=map {s{(\.\d{$size})\d*}{$1}g; s{[ ]+}{ }g; $_}
map {sprintf "%s", $_} @_;
return @a;
}
Define, lee y valida parámetros de la línea de comandos.
# name: parameters
my ($a,$b); # 2D basis.
my $c; # 3D Separation between sites in nearby planes
my $pqmax; # index of largest reciprocal vector
my $dmax; # index of largest distance to calculate
my $N; # seminumber of planes of film
my $digits=7; # number of decimal digits to print
my $options=q(
'a=s'=>\$a, # 2D basis vector x,y
'b=s'=>\$b, # 2D basis vector x,y
'c=s'=>\$c, # 3D separation x,y,z
'pqmax=i'=>\$pqmax, # index of largest reciprocal vector
'dmax=i'=>\$dmax, # index of largest distance to calculate
'N=i'=>\$N, # seminumber of planes of film
'digits=i'=>\$digits, # number of decimal digits to print
);
my %options=(eval $options);
die "Bad option definition: $@" if $@;
GetOptions(%options) or usage $options, "Bad options";
usage $options, "Undefined parameters"
unless lu_all {defined $_} ($a, $b, $c, $pqmax, $dmax, $N);
usage $options, "Vectors should be comma separated list of numbers"
unless lu_all {looks_like_number $_} map {split ','} ($a, $b, $c);
#convert from strings to vectors
($a,$b,$c) = map {pdl(split ',', $_)} ($a, $b, $c);
usage $options, "Basis vectors should be 2D"
unless lu_all {$_->dims==1 and $_->dim(0)==2} ($a, $b);
usage $options, "c should be 3D" unless $c->dims==1 and $c->dim(0)==3;
usage $options, "Third component of c should be positive"
unless $c->((2)) > 0;
usage $options, "pqmax should be positive" unless $pqmax > 0;
usage $options, "dmax should be positive" unless $dmax > 0;
usage $options, "N should be positive" unless $N > 0;
Calcula el área de la celda unitaria 2D 
, el volumen de la celda
unitaria 3D 
y la densidad
# name: area
my $A=($a->((0))*$b->((1))-$a->((1))*$b->((0)))->abs;
my $V=$A*$c->((2));
my $density=1/$V;
Genera la red recíproca 
, donde
son los elementos de la base dual,
. En 2D,
y
. En el programa
uso $a y $b para denotar la base y $Ga$ y ~$Gb para la base
dual.
# name: reciprocal
my ($a_perp, $b_perp)=map {pdl(-$_->((1)), $_->((0)))} ($a, $b);
my ($Ga, $Gb)=map {2*PI*$_->[0]/inner($_->[0], $_->[1])}
([$b_perp, $a], [$a_perp, $b]);
my $pq=zeroes(2*$pqmax+1,2*$pqmax+1)->ndcoords-$pqmax; #i,p,q
my $G=$pq->((0),*1)*$Ga+$pq->((1),*1)*$Gb; #i,p,q
Genera los vectores 3D 
.
# name: reciprocal-decay
my $G_abs=inner($G, $G)->sqrt; # p,q
my ($g_p, $g_m)=map {append($G, ($_*i()*$G_abs)->(*1))} (+1,-1); # i,p,q
Con ellos arma los tensores 
.
# name: T+-
# i,j,gx,gy
my ($T_p, $T_m)= map {-2*PI/$A*$_->(*1,:)*$_->(:,*1)/$G_abs->(*1,*1)}
($g_p, $g_m); # i,j,p,q
$_->(:,:,$pqmax,$pqmax).=0 foreach ($T_p, $T_m); # Fix division by 0
Ahora arma las interacciones 
para positiva y negativa.
# name: interactions
my $ns=sequence($dmax)+1; # n
my $exp_p=exp(i()*cinner($g_p, $c))**$ns->(*1,*1); #p,q,n
my $exp_m=exp(-i()*cinner($g_m, $c))**$ns->(*1,*1); #p,q,n
my $T_n0=($T_p #i,j,p,q
*$exp_p->(*1,*1)) #i,j,p,q,n
->mv(-2,0)->sumover->mv(-2,0)->sumover; #i,j,n
my $T_mn0=($T_m #i,j,p,q
*$exp_m->(*1,*1)) #i,j,p,q,n
->mv(-2,0)->sumover->mv(-2,0)->sumover; #i,j,n
Usa la regla de suma de las interacciones dipolares para obtener la autointeracción.
# name: selfinteraction
my $T_00 = 4*PI*$density/3*pdl([1,0,0],[0,1,0],[0,0,-2]) -
$T_n0->mv(-1,0)->sumover - $T_mn0->mv(-1,0)->sumover;
Arma las interacciones 
por bloques para una película
con 
planos. T_all tiene la interacción 
en el sitio
$N2+$n.
# name: interactions-film
my $N2=2*$N+1; # Number of planes
my $T_all=zeroes(cdouble, 3,3,2*$N2+1);
$T_all->(:,:,$N2+1:$N2+$dmax).=$T_n0;
$T_all->(:,:,$N2-1:$N2-$dmax).=$T_mn0;
$T_all->(:,:,($N2)).=$T_00;
my $T_nm=zeroes(cdouble,3,3,$N2,$N2);
for my $n(0..$N2-1){
for my $m(0..$N2-1){
$T_nm->(:,:,($n),($m)).=$T_all(:,:,($n-$m+$N2));
}
}
Arma las interacciones faltantes para la misma película. Estas son
para 
menor a cero o mayor al ancho de la
película. Entonces, para los sitios 
, 
y
para los sitios 
, 
, correspondientes a
los rangos $N2+$n1+1:2*$N2 y 0:$n de $T_all.
# name: missing
my $M_n=zeroes(cdouble,3,3,$N2);
for my $n(0..$N2-1){
$M_n->(:,:,($n)).=
$T_all->(:,:,$N2+$n+1:2*$N2)->mv(-1,0)->sumover
+$T_all(:,:,0:$n)->mv(-1,0)->sumover;
}
Con estos pedazos podemos armar un primer programa que calcula y reporta las interacciones para una película.
# name: interactions.pl
<<init>>
<<usage>>
<<cinner>>
<<trunc>>
<<parameters>>
<<area>>
<<reciprocal>>
<<reciprocal-decay>>
<<T+->>
<<interactions>>
<<selfinteraction>>
<<interactions-film>>
<<missing>>
my @dir=qw(xx yy zz);
say "Diagonal components of the interaction";
say "$dir[$_]: ", trunc $digits, $T_nm->(($_),($_)) for (0..2);
say "Missing terms due to surface";
say "$dir[$_]: ", trunc $digits,$M_n->(($_),($_)) for (0..2);
Podemos correrlo como a continuación para la superficie 
de
una red cúbica 
, 
, truncando
la red recíproca en 
, permitiendo interacciones con
segundos vecinos y en una película de semiancho 3 (ancho 7):
./interactions.pl -a 1,0 -b 0,1 -c 0,0,1 -pqmax 2 -dmax 2 -N 3 -digits 4
Resultados:
Diagonal components of the interaction
xx:
[
[ 4.5168 -0.1637 -0.0002 0 0 0 0]
[ -0.1637 4.5168 -0.1637 -0.0002 0 0 0]
[-0.0002 -0.1637 4.5168 -0.1637 -0.0002 0 0]
[ 0 -0.0002 -0.1637 4.5168 -0.1637 -0.0002 0]
[ 0 0 -0.0002 -0.1637 4.5168 -0.1637 -0.0002]
[ 0 0 0 -0.0002 -0.1637 4.5168 -0.1637]
[ 0 0 0 0 -0.0002 -0.1637 4.5168]
]
yy:
[
[ 4.5168 -0.1637 -0.0002 0 0 0 0]
[ -0.1637 4.5168 -0.1637 -0.0002 0 0 0]
[-0.0002 -0.1637 4.5168 -0.1637 -0.0002 0 0]
[ 0 -0.0002 -0.1637 4.5168 -0.1637 -0.0002 0]
[ 0 0 -0.0002 -0.1637 4.5168 -0.1637 -0.0002]
[ 0 0 0 -0.0002 -0.1637 4.5168 -0.1637]
[ 0 0 0 0 -0.0002 -0.1637 4.5168]
]
zz:
[
[ -9.0336 0.3274 0.0005 0 0 0 0]
[ 0.3274 -9.0336 0.3274 0.0005 0 0 0]
[0.0005 0.3274 -9.0336 0.3274 0.0005 0 0]
[ 0 0.0005 0.3274 -9.0336 0.3274 0.0005 0]
[ 0 0 0.0005 0.3274 -9.0336 0.3274 0.0005]
[ 0 0 0 0.0005 0.3274 -9.0336 0.3274]
[ 0 0 0 0 0.0005 0.3274 -9.0336]
]
Missing terms due to surface
xx: [-0.1640 -0.0002 0 0 0 -0.0002 -0.1640]
yy: [-0.1640 -0.0002 0 0 0 -0.0002 -0.1640]
zz: [0.3280 0.0005 0 0 0 0.0005 0.3280]
Ahora repito el cálculo pero truncando la red recíproca en 
,
./interactions.pl -a 1,0 -b 0,1 -c 0,0,1 -pqmax 3 -dmax 3 -N 3 -digits 4
Resultados:
Diagonal components of the interaction
xx:
[
[ 4.5168 -0.1637 -0.0002 -5.1449e-07 0 0 0]
[ -0.1637 4.5168 -0.1637 -0.0002 -5.1449e-07 0 0]
[-0.0002 -0.1637 4.5168 -0.1637 -0.0002 -5.1449e-07 0]
[-5.1449e-07 -0.0002 -0.1637 4.5168 -0.1637 -0.0002 -5.1449e-07]
[ 0 -5.1449e-07 -0.0002 -0.1637 4.5168 -0.1637 -0.0002]
[ 0 0 -5.1449e-07 -0.0002 -0.1637 4.5168 -0.1637]
[ 0 0 0 -5.1449e-07 -0.0002 -0.1637 4.5168]
]
yy:
[
[ 4.5168 -0.1637 -0.0002 -5.1449e-07 0 0 0]
[ -0.1637 4.5168 -0.1637 -0.0002 -5.1449e-07 0 0]
[-0.0002 -0.1637 4.5168 -0.1637 -0.0002 -5.1449e-07 0]
[-5.1449e-07 -0.0002 -0.1637 4.5168 -0.1637 -0.0002 -5.1449e-07]
[ 0 -5.1449e-07 -0.0002 -0.1637 4.5168 -0.1637 -0.0002]
[ 0 0 -5.1449e-07 -0.0002 -0.1637 4.5168 -0.1637]
[ 0 0 0 -5.1449e-07 -0.0002 -0.1637 4.5168]
]
zz:
[
[ -9.0336 0.3274 0.0005 1.0289e-06 0 0 0]
[ 0.3274 -9.0336 0.3274 0.0005 1.0289e-06 0 0]
[0.0005 0.3274 -9.0336 0.3274 0.0005 1.0289e-06 0]
[1.0289e-06 0.0005 0.3274 -9.0336 0.3274 0.0005 1.0289e-06]
[ 0 1.0289e-06 0.0005 0.3274 -9.0336 0.3274 0.0005]
[ 0 0 1.0289e-06 0.0005 0.3274 -9.0336 0.3274]
[ 0 0 0 1.0289e-06 0.0005 0.3274 -9.0336]
]
Missing terms due to surface
xx: [-0.1640 -0.0002 -5.1449e-07 0 -5.1449e-07 -0.0002 -0.1640]
yy: [-0.1640 -0.0002 -5.1449e-07 0 -5.1449e-07 -0.0002 -0.1640]
zz: [0.3280 0.0005 1.0289e-06 0 1.0289e-06 0.0005 0.3280]
Comparando con los resultados previos, vemos que hay convergencia en la quinta cifra. Para otras orientaciones y otras redes podría requerirse el uso de más vectores recíprocos, pero siempre es un número muy modesto.
Polarización superficial
Con esto, ya podemos calcular las modificaciones superficiales a la polarización. Para esto, modificamos nuestra lista de parámetros para poder dar una respuesta dieléctrica y elegir una orientación.
# name: parameters2
my ($a,$b); # 2D basis.
my $c; # 3D Separation between sites in nearby planes
my $pqmax; # index of largest reciprocal vector
my $dmax; # index of largest distance to calculate
my $N; # seminumber of planes of film
my $direction; # cartesian direction, x y or z
my $epsilon; # dielectric function
my $digits=7; # number of decimal digits to print
my $options=q(
'a=s'=>\$a, # 2D basis vector x,y
'b=s'=>\$b, # 2D basis vector x,y
'c=s'=>\$c, # 3D separation x,y,z
'pqmax=i'=>\$pqmax, # index of largest reciprocal vector
'dmax=i'=>\$dmax, # index of largest distance to calculate
'N=i'=>\$N, # seminumber of planes of film
'dir=s'=>\$direction, # cartesian direction, x y or z
'epsilon=s'=>\$epsilon, # dielectric function e',e''
'digits=i'=>\$digits, # number of decimal digits to print
);
my %options=(eval $options);
die "Bad option definition: $@" if $@;
GetOptions(%options) or usage $options, "Bad options";
usage $options, "Undefined parameters"
unless lu_all {defined $_}
($a, $b, $c, $pqmax, $dmax, $N, $direction, $epsilon);
usage $options, "Vectors should be comma separated list of numbers"
unless lu_all {looks_like_number $_} map {split ','} ($a, $b, $c);
#convert from strings to vectors
($a,$b,$c) = map {pdl(split ',', $_)} ($a, $b, $c);
usage $options, "Basis vectors should be 2D"
unless lu_all {$_->dims==1 and $_->dim(0)==2} ($a, $b);
usage $options, "c should be 3D" unless $c->dims==1 and $c->dim(0)==3;
usage $options, "Third component of c should be positive"
unless $c->((2)) > 0;
usage $options, "pqmax should be positive" unless $pqmax > 0;
usage $options, "dmax should be positive" unless $dmax > 0;
usage $options, "dir should be x, y or z"
unless $direction=~m{^[xyzXYZ]$};
my %index_from_direction=(x=>0, y=>1, z=>2);
my $dir_i=$index_from_direction{lc $direction};
usage $options, "N should be positive" unless $N > 0;
usage $options, "epsilon should be two comma separated numbers eps', eps''"
unless lu_all {looks_like_number $_} split ',', $epsilon;
$epsilon=[split ',', $epsilon];
$epsilon=$epsilon->[0]+i()*$epsilon->[1];
Dado un campo externo normalizado 
, podemos obtener la polarización de
bulto 
y el dipolo de bulto 
.
# name: pB
my $PB=$dir_i==2?(1-1/$epsilon)/(4*PI):($epsilon-1)/(4*PI);
my $pB=$PB/$density; # dipole moment
Usando Claussius Mossoti 
también podemos obtener la polarizabilidad ,
# name: alpha
my $alpha=3/(4*PI*$density)*($epsilon-1)/($epsilon+2);
La ecuación a resolver es
17
La ecuación en el bulto es
18
Restando,
19
que reescribimos como
20
donde 
es el tensor identidad y 
es la suma de las interacciones con
los planos ausentes.
Construimos entonces rutinas para resolver sistemas lineales de ecuaciones complejas, basadas en rutinas estandard reales. Hacemos una descomposición LU y la usamos para resolver la ecuación.
# name: lu
sub solve {
my ($Matrix, $rhs)=@_;
#Convert complex equation to real equation
my ($Mr, $Mi)=($Matrix->re, $Matrix->im);
my $N=$Mr->dim(0);
my $real_M=pdl($Mr,-$Mi, $Mi, $Mr)->reshape($N,$N,2,2)
->mv(2,1)->reshape(2*$N,2*$N); #assumed no extra dims.
my $real_rhs=append($rhs->re, $rhs->im)->dummy(1); #make row vector
my ($lu,$perm,$par) = $real_M->copy->lu_decomp;
my $real_sol=lu_backsub($lu, $perm, $real_rhs->copy); #returns row
my $sol=$real_sol->(0:$N-1,(0))+i()*$real_sol->($N:2*$N-1,(0));
$sol; #ordinary complex vector
}
Finalmente, usamos estas rutinas para resolver el sistema lineal de ecuaciones.
# name: Dp
my $identity=$T_nm->(($dir_i),($dir_i))->zeroes;
$identity->diagonal(0,1)++;
my $Dp=solve($identity-$alpha*$T_nm->(($dir_i),($dir_i)),
-$alpha*$M_n->(($dir_i),($dir_i))*$pB);
Armamos el programa juntando los fragmentos,
# name Delta p
<<init>>
<<usage>>
<<cinner>>
<<trunc>>
<<lu>>
<<parameters2>>
<<area>>
<<reciprocal>>
<<reciprocal-decay>>
<<T+->>
<<interactions>>
<<selfinteraction>>
<<interactions-film>>
<<missing>>
<<pB>>
<<alpha>>
<<Dp>>
say trunc $digits, $Dp;
Probémoslo con un dieléctrico no disipativo.
./Delta_p.pl -a 1,0 -b 0,1 -c 0,0,1 -pqmax 2 -dmax 2 -N 5 -dir x \
-epsilon 2,0 -digits 4
Resultados:
[0.0010 -1.2466e-05 1.4262e-07 -1.6256e-09 1.8520e-11 -4.2182e-13
1.8520e-11 -1.6256e-09 1.4262e-07 -1.2466e-05 0.0010]
Ahora, con vacío + disipación
./Delta_p.pl -a 1,0 -b 0,1 -c 0,0,1 -pqmax 2 -dmax 2 -N 5 -dir x \
-epsilon 1,1 -digits 4
Resultados:
[-0.0010-2.7054e-05i -2.4601e-06+1.3453e-05i 1.7311e-07+5.9471e-08i
1.1283e-09-2.1714e-09i -2.6469e-11-1.9207e-11i -6.1268e-13+6.2393e-13i
-2.6469e-11-1.9207e-11i 1.1283e-09-2.1714e-09i 1.7311e-07+5.9471e-08i
-2.4601e-06+1.3453e-05i -0.0010-2.7054e-05i]
Sistema semiinfinito.
Podemos simular un sistema semiinfinito como una película finita,
suficientemente ancha y eliminando el término que fuerza al sistema
por uno de los lados, i.e. redefiniendo las 
’s. Para ello,
modificamos el bloque missing.
# name: missing1
my $M_n=zeroes(cdouble,3,3,$N2);
for my $n(0..$N2-1){
$M_n->(:,:,($n)).=
$T_all->(:,:,$N2+$n+1:2*$N2)->mv(-1,0)->sumover;
}
Con esto armamos un nuevo programa.
# name Delta p1
<<init>>
<<usage>>
<<cinner>>
<<trunc>>
<<lu>>
<<parameters2>>
<<area>>
<<reciprocal>>
<<reciprocal-decay>>
<<T+->>
<<interactions>>
<<selfinteraction>>
<<interactions-film>>
<<missing1>>
<<pB>>
<<alpha>>
<<Dp>>
say trunc $digits, $Dp;
Le aplicamos las mismas pruebas que arriba.
./Delta_p1.pl -a 1,0 -b 0,1 -c 0,0,1 -pqmax 2 -dmax 2 -N 5 -dir x \
-epsilon 2,0 -digits 4
Resultados:
[0.0010 -1.2466e-05 1.4262e-07 -1.6256e-09 1.8517e-11 -2.1091e-13
2.4021e-15 -2.7358e-17 3.1159e-19 -3.5489e-21 4.0413e-23]
./Delta_p1.pl -a 1,0 -b 0,1 -c 0,0,1 -pqmax 2 -dmax 2 -N 5 -dir x \
-epsilon 1,1 -digits 4
Resultados:
[-0.0010-2.7054e-05i -2.4601e-06+1.3453e-05i 1.7311e-07+5.9471e-08i
1.1283e-09-2.1714e-09i -2.6473e-11-1.9211e-11i -3.0634e-13+3.1196e-13i
3.5181e-15+4.6669e-15i 6.8655e-17-3.7276e-17i -3.5698e-19-9.8135e-19i
-1.3679e-20+2.7779e-21i 9.6595e-24+1.8636e-22i]
Comparando con los resultados de la sección anterior vemos que 
es esencialmente idéntica al caso anterior cerca de la superficie
mientras que ahora se hace prácticamente cero en el otro extremo.
Respuesta superficial
Ahora podemos promediar el exceso de polarización sobre la celda unitaria e integrarla sobre la coordenada normal para obtener la corriente superficial
21
De aquí podemos identificar las conductividades superficiales,
22
donde 
es el área de la celda unitaria 2D, supusimos que 
, 
,
y son direcciones principales y que
usamos campos normalizados 
al calcular 
, 
y 
al
calcular 
.
Con estas funciones respuesta puedo calcular la impedancia superficial
23
donde elegimos las componentes apropiadas de acuerdo a la polarización y a la orientación del plano de incidencia.
Por motivos prácticos tenemos que enfrentar ahora el problema de las
unidades. En general, 
, 
, por
lo que 
y los cocientes 
y 
son adimensionales. Al normalizar los campos a 1 y desproveerlos de unidades,
los dipolos calculados arriba tendrían unidades de volumen en lugar de
carga por distancia, puesto que la polarizabilidad tiene unidades de
volumen. Al dividirlos entre adquirirían unidades de distancia y
al multiplicarlos por 
llegaríamos a las esperadas unidades de
velocidad. Es común expresar la frecuencia en términos de la energía
en unidades de 
. Por otro lado, es cómodo expresar
los vectores de la base cristalina 
, 
y en
unidades del parámetro de red del sistema. Entonces, la velocidad de la luz arriba
deberíamos expresarla en unidades consistentes, por ejemplo,
eV 
parámetro de red. Para ello usamos el factor de conversión
e leemos el parámetro de red en
nanómetros de la línea de comandos.
Modificamos entonces una vez más nuestra lista de parámetros, añadiendo el factor de corrección, el parámetro de red y la frecuencia, quitando una dirección específica para iterar sobre todas.
# name: parameters3
use constant hbar_c=>197.3; # eV nm
my ($a,$b); # 2D basis.
my $c; # 3D Separation between sites in nearby planes
my $pqmax; # index of largest reciprocal vector
my $dmax; # index of largest distance to calculate
my $N; # seminumber of planes of film
my $epsilon; # dielectric function
my $lattice; #lattice parameter in nm
my $hbar_w; # frequency in eV
my $digits=7; # number of decimal digits to print
my $options=q(
'a=s'=>\$a, # 2D basis vector x,y
'b=s'=>\$b, # 2D basis vector x,y
'c=s'=>\$c, # 3D separation x,y,z
'pqmax=i'=>\$pqmax, # index of largest reciprocal vector
'dmax=i'=>\$dmax, # index of largest distance to calculate
'N=i'=>\$N, # seminumber of planes of film
'epsilon=s'=>\$epsilon, # dielectric function e',e''
'lattice=f'=>\$lattice, #lattice parameter in nm
'frequency=f'=>\$hbar_w, # frequency in eV
'digits=i'=>\$digits, # number of decimal digits to print
);
my %options=(eval $options);
die "Bad option definition: $@" if $@;
GetOptions(%options) or usage $options, "Bad options";
usage $options, "Undefined parameters"
unless lu_all {defined $_}
($a, $b, $c, $pqmax, $dmax, $N, $epsilon,
$lattice, $hbar_w);
usage $options, "Vectors should be comma separated list of numbers"
unless lu_all {looks_like_number $_} map {split ','} ($a, $b, $c);
#convert strings->vectors
($a,$b,$c) = map {pdl(split ',', $_)} ($a, $b, $c);
usage $options, "Basis vectors should be 2D"
unless lu_all {$_->dims==1 and $_->dim(0)==2} ($a, $b);
usage $options, "c should be 3D" unless $c->dims==1 and $c->dim(0)==3;
usage $options, "Third component of c should be positive"
unless $c->((2)) > 0;
usage $options, "pqmax should be positive" unless $pqmax > 0;
usage $options, "dmax should be positive" unless $dmax > 0;
usage $options, "N should be positive" unless $N > 0;
usage $options,
"epsilon should be two comma separated numbers eps', eps''"
unless lu_all {looks_like_number $_} split ',', $epsilon;
$epsilon=[split ',', $epsilon];
$epsilon=$epsilon->[0]+i()*$epsilon->[1];
Ahora calculamos las tres conductividades normalizadas,
# name: sigmas
my @sigma= map {
my $PB=$_==2?(1-1/$epsilon)/(4*PI):($epsilon-1)/(4*PI);
my $pB=$PB/$density; # dipole moment
my $identity=$T_nm->(($_),($_))->zeroes;
$identity->diagonal(0,1)++;
my $Dp=solve($identity-$alpha*$T_nm->(($_),($_)),
-$alpha*$M_n->(($_),($_))*$pB);
-i()*$hbar_w*$lattice*$Dp->sumover/(hbar_c*$A);
} (0..2);
Con esto armamos un nuevo programa.
# name sigma
<<init>>
<<usage>>
<<cinner>>
<<trunc>>
<<lu>>
<<parameters3>>
<<area>>
<<reciprocal>>
<<reciprocal-decay>>
<<T+->>
<<interactions>>
<<selfinteraction>>
<<interactions-film>>
<<missing1>>
<<alpha>>
<<sigmas>>
my @dirs_from_index=qw(xx yy zz);
say "$dirs_from_index[$_]: $sigma[$_]" for (0..2);
Ahora lo corremos para un aislante en una red cúbica simple.
./sigma.pl -a 1,0 -b 0,1 -c 0,0,1 -pqmax 2 -dmax 2\
-N 5 -epsilon 2,0 -lattice .4 -frequency 10 -digits 4
Resultados:
xx: -2.13738209040293e-05i
yy: -2.13738209040293e-05i
zz: 1.04118689039735e-05i
Reflectancia diferencial
Tenemos ya prácticamente todas las herramientas para calcular los
cambios en la reflectancia. Para ello, en lugar de leer un valor de
desde la línea de comandos, leeremos el nombre de un
archivo con una tabla de valores de frecuencia, 
y
para, y para cada valor obtendremos la impedancia
superficial, la conductividad superficial y la reflectancia. A la
lista de parámetros hay que añadir el nombre del archivo, el ángulo
de incidencia y el nombre del archivo de salida.
# name: parameters4
use constant hbar_c=>197.3; # eV nm
my ($a,$b); # 2D basis.
my $c; # 3D Separation between sites in nearby planes
my $pqmax; # index of largest reciprocal vector
my $dmax; # index of largest distance to calculate
my $N; # seminumber of planes of film
my $lattice; #lattice parameter in nm
my $angle; #incidence angle (degrees)
my $ifilename; # name of input file: hnu eps' eps''
my $title; # title of the output plot
my $ofilename; # name of output plot (png)
my $digits=7; # number of decimal digits to print
my $options=q(
'a=s'=>\$a, # 2D basis vector x,y
'b=s'=>\$b, # 2D basis vector x,y
'c=s'=>\$c, # 3D separation x,y,z
'pqmax=i'=>\$pqmax, # index of largest reciprocal vector
'dmax=i'=>\$dmax, # index of largest distance to calculate
'N=i'=>\$N, # seminumber of planes of film
'lattice=f'=>\$lattice, #lattice parameter in nm
'angle=f'=>\$angle, #incidence angle (degrees)
'ifilename=s'=>\$ifilename, # name of input file: hnu eps' eps''
'ofilename=s'=>\$ofilename, # name of output plot (png)
'title=s'=>\$title, # title of the output plot
'digits=i'=>\$digits, # number of decimal digits to print
);
my %options=(eval $options);
die "Bad option definition: $@" if $@;
GetOptions(%options) or usage $options, "Bad options";
usage $options, "Undefined parameters"
unless lu_all {defined $_}
($a, $b, $c, $pqmax, $dmax, $N, $lattice, $angle, $ifilename,
$ofilename, $title);
usage $options, "Vectors should be comma separated list of numbers"
unless lu_all {looks_like_number $_} map {split ','} ($a, $b, $c);
#convert strings->vectors
($a,$b,$c) = map {pdl(split ',', $_)} ($a, $b, $c);
usage $options, "Basis vectors should be 2D"
unless lu_all {$_->dims==1 and $_->dim(0)==2} ($a, $b);
usage $options, "c should be 3D" unless $c->dims==1 and $c->dim(0)==3;
usage $options, "Third component of c should be positive"
unless $c->((2)) > 0;
usage $options, "pqmax should be positive" unless $pqmax > 0;
usage $options, "dmax should be positive" unless $dmax > 0;
usage $options, "N should be positive" unless $N > 0;
usage $options, "Angle should be between 0 and 90"
unless $angle >=0 and $angle < 90;
my $angler=$angle*PI/180; # angle in radians
usage $options, "ifilename should be readable" unless -r $ifilename;
# frequency in eV, real, imag and full dielectric function
my ($hbar_ws, $epsilons1, $epsilons2)=rcols $ifilename;
usage $options,
"File should have three columns of space separated numbers"
unless $hbar_ws->dim(0)==$epsilons1->dim(0) and
$hbar_ws->dim(0)==$epsilons2->dim(0) and $hbar_ws->dim(0) > 0;
my $epsilons=$epsilons1+i()*$epsilons2;
Aprovechando que en PDL, rutinas diseñadas para actuar sobre un
escalar se pueden aplicar a arreglos multidimensionales sin
modificación, entonces el fragmento alpha puede ser usado sin
modificación. Sin embargo, los fragmentos lu y sigma si deben modificarse
para acomodar la nueva dimensión (la frecuencia). Aunque no es lo más
elegante, podemos evitarlo y reciclar los fragmentos previos si
hacemos una iteración. Una solución más elegante hubiera sido preveer
el reciclar cada fragmento construyéndolo como módulos a usar o como
subrutinas con argumentos en lugar de ser fragmentos a incorporar en un código
lineal (de espageti) y comunicarnos mediante el nombre de las
variables. Es el precio a pagar por armar el código
incrementalmente. Dentro cada iteración podemos también calculamos la
impedancia superficial y la reflectancia.
Primero calculo la impedancia superficial no perturbada, la impedancia perturbada, la amplitud de reflexión y la reflectancia.
# name DR/R
my $q=1+0*i(); # normalize to free wavevector
my $Q=$q*sin($angler);
my ($kv, $km)= map {mysqrt($_*$q**2-$Q**2)} (1, $epsilon);
my ($Zsv, $Zpv)= ($q/$kv, $kv/$q);
my ($Zsm0, $Zpm0)= ($q/$km, $km/($q*$epsilon));
my @Zsm=map {$Zsm0/(1+4*PI*$Zsm0*$_)} @sigma[0,1];
my @Zpm=map {($Zpm0+4*PI*$Q**2/$q**2*$sigma[2])/(1+4*PI*$Zpm0*$_)}
@sigma[0,1];
#perturbed and non perturbed
my ($rs0,@rs)=map {($_-$Zsv)/($_+$Zsv)} $Zsm0, @Zsm;
my ($rp0,@rp)=map {($Zpv-$_)/($Zpv+$_)} $Zpm0, @Zpm;
my ($Rs0,@Rs)=map {$_->abs**2} ($rs0,@rs);
my ($Rp0,@Rp)=map {$_->abs**2} ($rp0,@rp);
my @DRRs=map {($Rs[$_]-$Rs0)/$Rs0} (0,1); #differential
my @DRRp=map {($Rp[$_]-$Rp0)/$Rp0} (0,1);
El cálculo de la impedancia requiere una nueva rutina de utilería
mysqrt; como la raiz cuadrada tiene dos ramas, debo escoger aquella
con parte imaginaria no negativa, i.e., colocando el corte ramal justo
abajo del eje positivo.
# name mysqrt
sub mysqrt {
my $x2=shift @_;
my $x=sqrt($x2);
$x=-$x if $x->im <0;
return $x;
}
# name DeltaR
<<init>>
<<usage>>
<<cinner>>
<<trunc>>
<<mysqrt>>
<<lu>>
<<parameters4>>
<<area>>
<<reciprocal>>
<<reciprocal-decay>>
<<T+->>
<<interactions>>
<<selfinteraction>>
<<interactions-film>>
<<missing1>>
use PDL::Graphics::Gnuplot;
my @results; # accumulate results
for my $r(0..$hbar_ws->dim(0)-1){ # iterate over rows
my $hbar_w=$hbar_ws->(($r));
my $epsilon=$epsilons->(($r));
<<alpha>>
<<sigmas>>
<<DR/R>>
push @results, [$hbar_w, @DRRs, @DRRp];
}
my ($hbar_w, $DRRsx, $DRRsy, $DRRpx, $DRRpy)=
map {my $i=$_; pdl(map {$_->[$i]} @results)} (0..4);
my $win=gpwin("png", output=>$ofilename);
$win->plot({title=>$title, xlabel=>'Frecuencia (eV)',
ylabel=>'Anisotropía {/Symbol D}R/R'},
{with=>'lines', legend=>'Pol S'}, $hbar_w, $DRRsx-$DRRsy,
{with=>'lines', legend=>'Pol P'}, $hbar_w, $DRRpx-$DRRpy);
Ahora corremos el cálculo para la cara (110) del Si.
./DeltaR.pl -a .7071,0 -b 0,1 -c .3536,.5,.3536 \
-pqmax 3 -dmax 5 -N 5 -lattice .54 -angle 0 \
-ifilename epsSiAsp.dat -ofilename si110.png \
-title 'Anisotropía (R_y-R_x)/R para Si (110) Incidencia normal'
Los resultados quedan en la siguiente gráfica
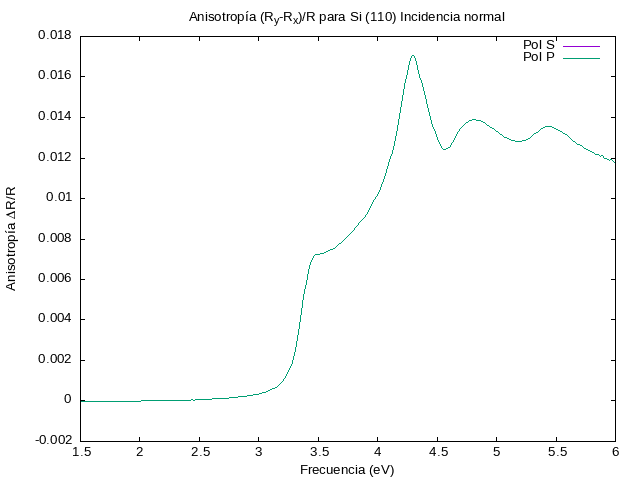
Lo volvemos a correr pero ahora a un ángulo de incidencia 
.
./DeltaR.pl -a .7071,0 -b 0,1 -c .3536,.5,.3536 \
-pqmax 3 -dmax 5 -N 5 -lattice .54 -angle 45 \
-ifilename epsSiAsp.dat -ofilename si110-45.png \
-title 'Anisotropía (R_y-R_x)/R para Si (110) {/Symbol Q}_i=45'
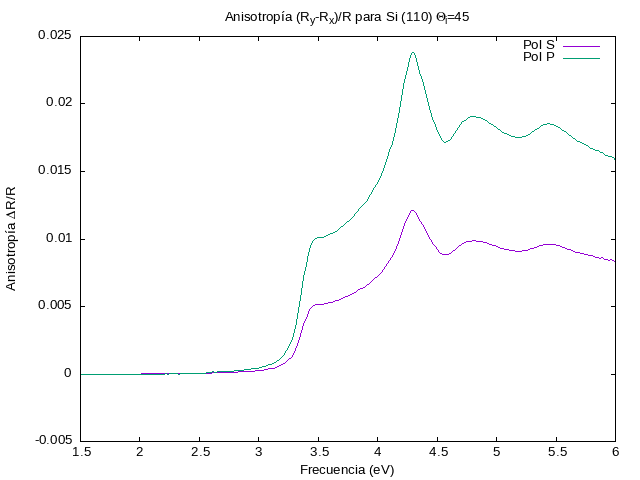
Curiosamente, aunque la respuesta normal es la misma para ambas
polarizaciones, como 
es menor, la anisotropía relativa es
mayor.
Conclusiones
Partimos de una idea muy simple, el efecto de campo local no tiene por qué ser idéntico en la vecindad de una superficie que en su interior. Para exporar las consecuencias desarrollamos una técnica para calcular la suma de interacciones dipolares por planos, discutimos cómo calcular la autointeracción de cada plano, y luego hallamos y resolvimos las ecuaciones que cumple el exceso de momento dipolar de cada sitio por hallarse cerca de la superficie y con el mismo, obtuvimos la conductividad superficial, la impedancia superficial y finalmente la reflectancia. Esta resulta tener una pequeña dependencia con la cara cristalina iluminada, y en el caso de caras anisotrópicas, con la polarización de la luz incidente. En este último caso, hay una anisotropía óptica inducida por la superficie en sistemas nominalmente isotrópicos. Como esta anisotropía se produce en las primeras camadas atómicas, su valor y la estructura de sus espectros dependen fuertemente de la condición de la superficie, y es fuertemente modificada por la presencia de adsorbatos, por la relajación y la reconstrucción superficial, por los cambios a la estructura electrónica, por la presencia de estados de superficie, por su modulación mediante campos externos y por los cambios de composición química. Esto permite que la espectroscopía de anisotropía en la reflectancia, conocida como RAS, sea empleada como una herramienta para observar superficies tanto dentro como fuera de cámaras de ultra-alto vacío, e incluso en ambientes químicamente hostiles. RAS se ha convertido en una espectroscopía óptica empleada rutinariamente en la industria semiconductora para monitorear la cinemática y para entender la dinámica del crecimiento epitaxial, así como para observar un sinnúmero de procesos superficiales.
Notas
Para preparar estas notas usé el editor extensible emacs y su modo
Org mode, el cual permite escribir con facilidad un texto
estructurado (artículo, libro, página web), incluyendo en él
fragmentos de código computacional que pueden ensamblarse
automáticamente, correrse y desplegar sus resultados en el mismo
archivo. Los programas fueron escritos en el lenguaje Perl y su
extensión numérica Perl Data Language.